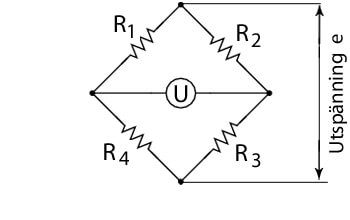
En wheatstonebrygga är en elektrisk krets lämplig för detektering av små resistansförändringar. Den används därför för att mäta resistansförändringar för en trådtöjningsgivare. Bryggan konfigureras genom att kombinera fyra motstånd som visas i figuren till höger.
Anta att:
R1 = R2 = R3 = R4, eller R1 • R3 = R2 • R4
Med denna koppling så får man oavsett vilken spänning som appliceras på ingången en utgångsspänning som är noll (0). Man säger att bryggan är i ”balans”. När denna jämvikt rubbas och wheatstonebryggan är i ”obalans” så får man en spänning på utgången som är proportionell mot resistansförändringen.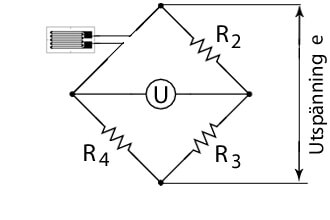
Som visas i figuren till höger så är en trådtöjningsgivare ansluten istället för R1 i kretsen. När givaren tar upp trådtöjningen och därmed initierar en resistansförändring ΔR, så ger bryggan ut en motsvarande elektrisk spänning, e.
Då vi enlig tidigare resonemang vet att ΔR/R = K • ε så kan vi skriva:
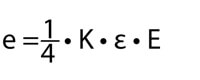
Och då alla värden förutom e är kända värden, kan töjningen ε bestämmas.
Olika bryggkopplingar
Kopplingen som beskrivs ovan kallas ett (1)-givarsystem då endast en givare är ansluten till wheatstonebryggan. Förutom 1-givarsystemet finns det 2- och 4-givarsystem.
2-givarsystem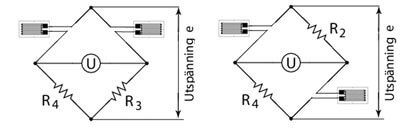
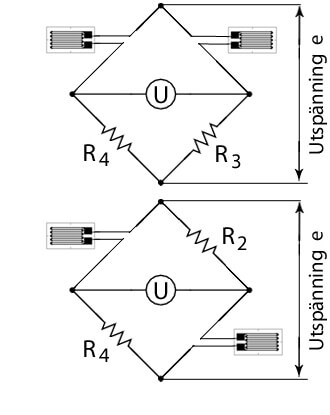
Med ett 2-givarsystem är trådtöjningsgivarna anslutna till bryggan på något av de två sätt som visas i figuren till höger.
Utspänning från ett 4-givarsystem
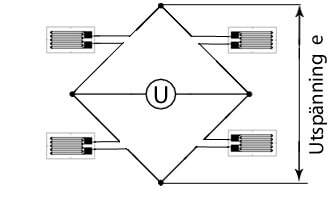4-givarsystemet har fyra givare anslutna till varsin sida av de fyra sidorna av bryggan. Denna koppling används sällan för töjningsmätningar men däremot ofta för trådtöjningsgivare. När givarna på de fyra sidorna har fått sitt motstånd ändrat till R1 + ΔR1, R2 + ΔR2, R3 + ΔR3 och R4 + ΔR4, så är bryggans utspänning, e:
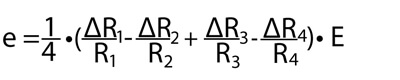
Om resistansen och givarfaktorn K för givarna på de fyra sidorna är lika och de utsätts för töjningarna ε1, ε2, ε3 och ε4 blir ekvationen:
Utspänning från ett 1-givarsystem
För ett 1-givarsystem sker däremot en motståndsförändring, R1, endast på ena sidan. Således är utspänningen:
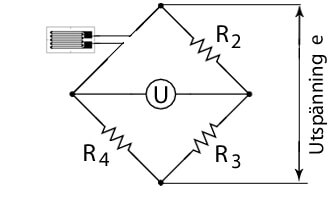
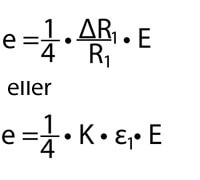
Generella töjningsmätningar utförs ofta med hjälp av ett 1-givarsystem.
Utspänning från ett 2-givarsystem
För ett 2-givarsystem är det två sidor som står för resistansförändringen. Således erhålls följande utspänning, se alt.1 i figuren till höger:
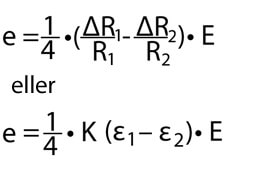
Även följande utspänning kan fås, se alt.2 i figuren till höger:
Ovanstående ekvationer ger alltså information om att den töjning som upptas av den andra givaren subtraheras eller adderas till den töjning som tas upp av den första givaren beroende på om givare två (R2) är inkopplad i intilliggande eller motsatta sida till givare ett (R1).
Tillämpning av 2-givarsystem
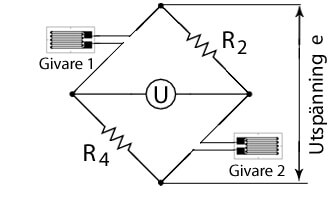
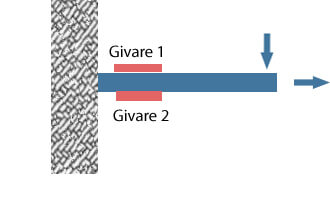2-givarsystemet används mest för följande tillämpning. För att mäta om en böjnings- eller dragspänning uppstår då en extern kraft påverkar en balk som är fixerad i ena änden. En töjningsgivare appliceras på ovansidan och en på undersidan, mitt emot varandra, se figuren till höger.
Dessa två givare är anslutna till intilliggande eller motsatta sidor i bryggkopplingen och böjnings- eller dragtöjningen kan mätas separat. Det betyder att givare 1 känner av dragtöjningen (plus/förlängning) och givare 2 känner av kompressionstöjningen (minus/hoppressning). Det absoluta töjningsvärdet är detsamma oavsett polaritet, förutsatt att de två givarna är på samma avstånd ifrån änden av balken.
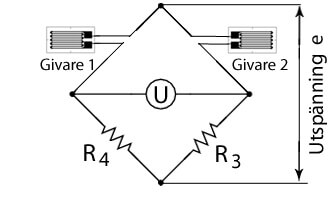För att mäta endast böjningstöjningen kan vi göra följande resonemang. Om givare 2, i förhållande till givare 1, ansluts till intilliggande sida, se figur till höger, så blir utspänningen i bryggkopplingen:
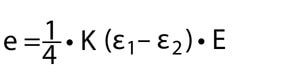
Då dragtöjningarna för givare 1 och 2 är plus och av samma i storlek så är (ε1 – ε2) i ekvationen lika med 0, och därigenom är också utspänningen e lika med 0. Däremot är böjningstöjningen för givare 1 plus och givare 2 minus, så ekvationen (ε1 – ε2) kan skrivas (ε1 – (- ε2)) vilket är (ε1 + ε2) och därigenom fördubblas utspänningen. Det vill säga att denna bryggkoppling endast möjliggör mätning av böjningstöjningen.
Om istället givare 2 är ansluten till motsatt sidan, se figuren till höger, så blir bryggkopplingens utspänning, e:
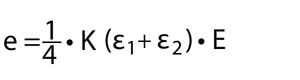
I detta fall blir utspänning således noll för böjningstöjningen medan den dubbleras för dragtöjningen. Det vill säga att denna bryggkoppling möjliggör endast mätning av dragtöjningen.
Temperatur
Resistiviteten är temperaturberoende hos alla ledarmaterial, läs vidare hur det påverkar en trådtöjningsgivare.